Poker Real Time Odds on Mac OS X: Part 3
The continuing story of creating a tool called SeeingStars, offering real time odds for PokerStars. Read part 1 and part 2.
Now the tricky stuff starts: having found the PokerStars table window, how do we determine the cards? This is not an easy programming problem. To make it easier, I’ll add some constraints. For the purpose of creating proof that real time odds is possible, here are the constraints I’m imposing:
- Heads-up only, so that we know there are always exactly two players in the hand.
- Maximum window size only, which is 1320 pixels by 932 pixels.
- Using PokerStars’ Nova theme, with green felt, 4-color deck, using the modern-style deck:
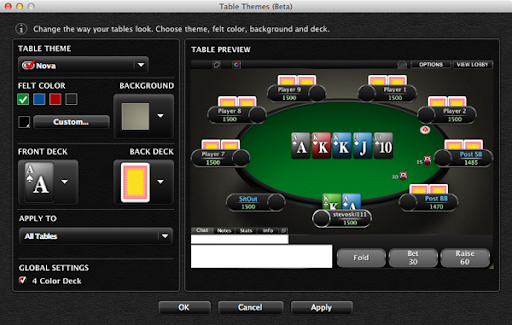
These constraints can be relaxed later, once I get the basics working.
Using the window id obtained in part 2 of this series we can get the screenshot:
- (NSBitmapImageRep *)createSingleWindowShot:(CGWindowID)windowID {
CGImageRef cgImageRef = CGWindowListCreateImage(
CGRectNull,
kCGWindowListOptionIncludingWindow,
windowID,
kCGWindowImageBoundsIgnoreFraming);
NSImage *const nsImage = [[NSImage alloc] initWithCGImage:cgImageRef size:NSZeroSize];
return [[NSBitmapImageRep alloc] initWithData:[nsImage TIFFRepresentation]];
}From the screen image we can determine the suit of a card by sampling the colour of one pixel. I used stackoverflow.com for information on finding the nearest colour to a pixel, and then map that colour to a suit. Some reading and experimentation shows the colour’s hue is a good method for differentiating between colours:
- (NSString *)getSuit:(NSBitmapImageRep *)bitmapImageRep x:(NSInteger)x y:(NSInteger)y {
NSDictionary *hues = @{
@0.57f:@"d",
@1.0f:@"d",
@0.29f:@"c",
@0.0f:@"s"
};
CGFloat pixelHue = ([bitmapImageRep colorAtX:x + 2 y:y + 4]).hueComponent;
double smallestDiff = fabs(0.38 - pixelHue); // 0.38 is the hue of the table felt
NSString *match = nil;
for (NSNumber *hue in hues.allKeys) {
const double diff = fabs((hue.floatValue) - pixelHue);
if (diff < smallestDiff) {
smallestDiff = diff;
match = [hues objectForKey:hue];
}
}
return match;
}
What about a card’s rank? This is harder. From experience I know that “thresholding” is helpful. Thresholding turns an image into a one-bit image: every pixel becomes either black or white, on or off, according to a threshold algorithm.
I started up Pixelmator and opened a PokerStars screenshot. Using Pixelmator’s threshold effect, I found that a setting of 80% worked well.
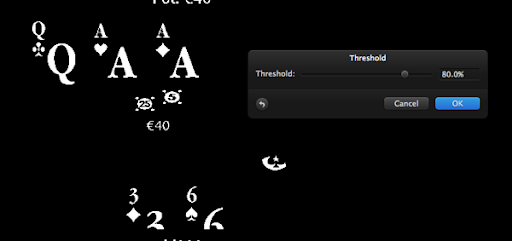
Most detail is gone, but the ranks of the cards are visible.
I turned this into Objective-C code:
- (BOOL)threshold:(NSColor *)color {
float value = 0.8f;
return color.redComponent > value &&
color.blueComponent > value &&
color.greenComponent > value;
}
- (void)logOneBitImage:(NSBitmapImageRep *)bitmapImageRep startX:(NSInteger)startX startY:(NSInteger)startY {
int width = 26;
int height = 30;
int ary[width * height];
for (int y = 0; y < height; y++) {
NSString *row = @"";
for (int x = 0; x < width; x++) {
NSColor *color = [bitmapImageRep colorAtX:x + startX y:y + startY];
ary[x * height + y] = [self threshold:color] ? 1 : 0;
row = [row stringByAppendingString:(ary[x * height + y]) == 0 ? @"0" : @"1"];
}
NSLog(@"row = %@", row);
}
NSLog(@" ");
}
This gives output in which you can clearly see the rank:
00000000000000000000000000
00000000011111000000000000
00000001110011110000000000
00000111100000111000000000
00001111000000111100000000
00001110000000011110000000
00011110000000011111000000
00011110000000001111000000
00011100000000001111000000
00111100000000001111000000
00111100000000001111000000
00111100000000001111100000
00111100000000000111100000
00111100000000001111000000
00111110000000001111000000
00011110000000001111000000
00011110000000001111000000
00001110000000001110000000
00001111000000011110000000
00000111100000011100000000
00000011110000111000000000
00000000111111100000000000
00000000001111000000000000
00000000001111000000000000
00000000001111100000000000
00000000001111110000000000
00000000000111111000000000
00000000000011111111000000
00000000000000011100000000
00000000000000000000000000
In the next article in this series, I’ll show how that set of 1’s and 0’s can be turned in a ‘Q’, in a reasonably fault-tolerant way.